As we know, a right triangle is a triangle whose one angle always measures 90°. The longest side opposite of a right triangle is called the hypotenuse, while the horizontal leg is called the base and the vertical leg is called the height or the altitude.
- A couple of problems about special right triangles Example #1: The legs of an isosceles right triangle measure 10 inches. Find the length of the hypotenuse. Since the triangle is isosceles, the legs are equal and we can use the formula. Hypotenuse = √(2)×(Leg) Hypotenuse =.
- Every right triangle has the property that the sum of the squares of the two legs is equal to the square of the hypotenuse (the longest side). The Pythagorean theorem is written: a2 + b2 = c2. What’s so special about the two right triangles shown here is that you have an even more special.
- Special right triangles are triangles whose sides are in a particular ratio, known as Pythagorean Triples. In geometry, the Pythagorean Theorem is a statement that shows the relationship of the sides of a right triangle.
May 12, 2013 Pythagorean theorem and special right triangles The Pythagorean Theorem can be used to prove that a 5-12-13 and 3-4-5 are right triangles. The Pythagorean Theorem states that the square of the hypotenuse is equal to the sum of the two sides squared. 3^2 + 4^2 = 5^2.

What is a Special Right Triangle
Special right triangles are right triangles whose angles or sides are in a particular ratio. They have some regular features that make calculations on it much easier.
In geometry, the Pythagorean Theorem is commonly used to find the relationship between the sides of a right triangle, given by the equation: a2 + b2 = c2, where a, b denotes the height and base of the triangle and c is the hypotenuse. But, if it is a special right triangle, we can use simpler formulas.
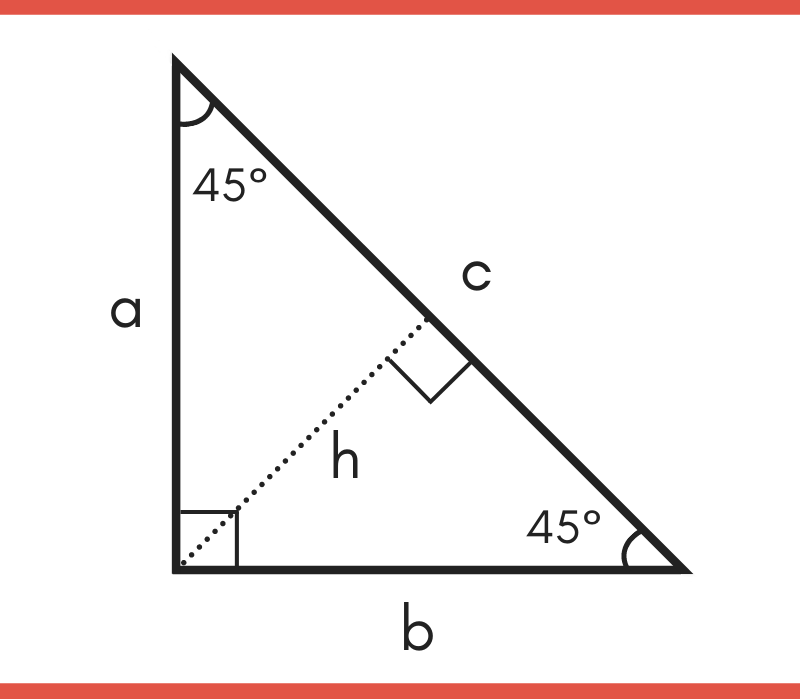
Some common special right triangles are shown below.
Types of Special Right Triangle
The two most common special right triangles are:
45-45-90 Triangle
A 45-45-90 triangle is a special right triangle whose three angles measure 45°, 45° and 90°. The ratio of its side lengths (base: height: hypotenuse) is 1: 1: √2.

30-60-90 Triangle
Special Right Triangles Formulas
A 30-60-90triangle is a special right triangle whose three angles measure 30°, 60° and 90°. The ratio of its side lengths (base: height: hypotenuse) is1: √3: 2.
Apart from the above two types, there are some other special right triangles.
Others: Pythagorean Triples
Some right triangles have sides that are of integer lengths and are collectively called the Pythagorean triples. Such triangles can be easily remembered and any multiple of the sides produces the same relationship. Pythagorean triples can be of three types:
- Common Pythagorean triples: Sides with integer lengths. Examples – 3-4-5, 5-12-13, 8-15-17, 7-24-25, and 9-40- 41.
- Almost-isosceles Pythagorean Triples: Sides with integer lengths but almost isosceles. Examples – 20-21-29, 119- 120-169, 696-697-985, and 4,059-4,060-5,741.
- Sides that are in Geometric Progression: Also known as the Kepler triangle, if the sides are in geometric progression a, ar, ar2, its common ratio r is given by r = √φ where φ is the golden ratio.
Formulas
Although there is no common formula for special right triangles, each of them has specific formulas for finding the missing sides, area, and perimeter based on the ratio of their side lengths. Find their formulas with solved examples in our separate articles.
How to Solve Special Right Triangles
Solving special right triangles is about finding the missing lengths of the sides. Instead of using the Pythagorean Theorem, we can simply use the special right triangle ratios to find the missing length. Let us understand the concept better by doing some practice problems.
The hypotenuse of a 45-45-90 triangle is 12√2 mm. Calculate the length of its base and height.
As we know,
Ratio of their Side Lengths = x: x: x√2, here x√2 = hypotenuse = 12√2 mm
Thus,
x√2 = 12√2 mm
Squaring both sides we get,
⇒ (x√2)2 = (12√2)2 mm
⇒ 2x2 = 144 x 2 = 288
⇒ x = √144 = 12 mm
Hence, the base and height of the given right triangle measure 16.97 mm each.
The longer side of a 30-60-90 right triangle is given by 5√3 cm. What is the measure of its shorter side and hypotenuse?
As we know,
Ratio of their Side Lengths = x: x√3: 2x, here x = shorter side, x√3 = longer side = 5√3 cm, 2x = hypotenuse
Thus,
x√3 = 5√3
Squaring both sides we get,
(x√3)2 = (5√3)2
⇒ 3x2 = 25 x 3
⇒ x2 = 25
⇒ x = 5 cm
The length of the hypotenuse and the other side of a right triangle are 30 cm and 24 cm, respectively. Find the length of the missing side.
Special Right Triangles 30 60 90
As we know,
Here we have to find whether the sides are in the ratio of 3x: 4x: 5x
Thus,
?: 24: 30 = ?: 4(6): 5(6)
Thus, the sides are in the ratio of 3x: 4x: 5x and it is a 3-4-5 triangle.
For calculating the third side,
For, n = 6
Hence, the length of the other side,
3x = 3 x 6 = 18
Therefore the length of the missing side is 18 cm.
If the two sides of a right triangle are 3 ft and 4 ft, find the length of hypotenuse.
Special Right Triangles Video
As we know,
Here we have to find whether the sides are in the ratio of 3x: 4x: 5x
3: 4: ? = 3(1): 4(1): ?
Thus, the sides are in the ratio of 3x: 4x: 5x and it is a 3-4-5 triangle
For calculating the hypotenuse,
For, n = 1
Hence, the length of the hypotenuse,
5x = 5 x 1 = 5
Therefore the length of the hypotenuse is 5 ft